Gerak Parabola

Gerak Proyektil

Mendefinsikan Proyektil

Proyektil adalah sebuah benda yang hanya mengalami gaya gravitasi. Ada banyak jenis proyektil. Sebuah benda yang jatuh dari keadaan diam adalah proyektil (asal hambatan udara dapat diabaikan). Sebuah benda yang dilemparkan ke atas juga merupakan proyektil (asal hambatan udara dapat diabaikan). Dan sebuah benda yang dilemparkan ke atas dengan sudut elevasi tertentu juga merupakan gerak proyektil (asal hambatan udaranya dapat diabaikan). A projectile is any object that once projected or dropped continues in motion by its own inertia and is influenced only by the downward force of gravity.

Tipe-tipe dari Proyektil

Diagram benda bebas proyektil

By definition, a projectile has a single force that acts upon it - the force of gravity. If there were any other force acting upon an object, then that object would not be a projectile. Thus, the free-body diagram of a projectile would show a single force acting downwards and labeled force of gravity (or simply F_grav). Regardless of whether a projectile is moving downwards, upwards, upwards and rightwards, or downwards and leftwards, the free-body diagram of the projectile is still as depicted in the diagram at the right. By definition, a projectile is any object upon which the only force is gravity.
 

Bayangkanlah sebuah meriam ditembakkan di tepi sebuah tebing yang sangat curam. Anggaplah di sini peluru meriam tidak mengalami hambatan udara yang berarti. Bagaimanakah lintasan dari peluru meriam selanjutnya dan bagaimana cara kita menggambarkannya? Animasi di bawah ini menggambarkan situasi tersebut. Dalam animasi tersebut lintasan peluru meriam juga diperlihatkan; sebagai tambahan, komponen kecepatan horizontal dan vertikal juga ditampilkan berupa anak panah dalam animasi.

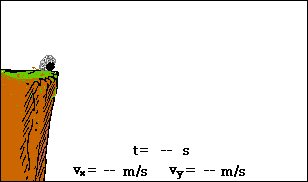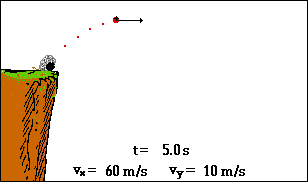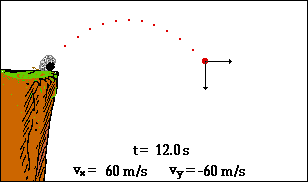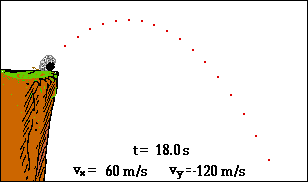
Sebagaimana tampak dari animasi tersebut, peluru meriam mengikuti lintasan Parabola. Ketika peluru naik menuju puncaknya, ia juga mengalami percepatan arah ke bawah. Peluru yang naik lalu diperlambat tersebut dikatakan tengah mengalami percepatan ke bawah.

Dalam animasi, percepatan arah ke bawah ini ditunjukkan oleh perubahan komponen vertikal kecepatan. Percepatan arah ke bawah ini disebabkan oleh gaya gravitasi arah ke bawah yang bekerja pada peluru. Jika gerak peluru meriam dapat didekati sebagai gerak proyektil  (yakni jika pengaruh hambatan udara dapat diabaikan), maka tidak akan ada percepatan arah horizontal. Dalam animasi ini ditunjukkan dengan konstannya vektor kecepatan pada arah horizontal.

Gerak proyektil/peluru adalah gerak di bawah pengaruh gravitasi. Jika kita berdiri di tepi sebuah gedung dan melempar sebuah bola pada suatu sudut, sesaat peluru akan bergerak  ke atas dan turun kemudian vertikal seraya tetap bergerak horizontal.

Gerak seperti ini disebut gerak proyektil/peluru atau gerak parabola.

Untuk lebih memahami gerak peluru ini, andaikan kita balik ke belakang dan melihat melalui dua sudut pandang pengamat yang berbeda.
Bagaimanakah gerak terlihat oleh pengamat yang jauh ?

Pengamat ini cukup jauh sehingga kehilangan pencerapan akan lebar namun masih dapat melihat dengan jelas bola naik dan turun.  Dari perspektif ini gerak merupakan gerak vertikal dengan percepatan konstan.

Bagaimana dengan pengamat yang melihat dari ketinggian? Pengamat ini cukup tinggi posisinya sehingga kehilangan persefsi akan kedalaman namun masih dapat melihat dengan jelas bola bergerak secara horizontal. Dalam hal ini dia mengamati dari perspektif gerak horizontal dengan kecepatan konstan.

Gerak peluru adalah kombinasi gerak vertikal dengan percepatan konstan (gerak jatuh bebas) dan gerak horizontal dengan kecepatan konstan (GLB).

---

Contoh Untuk mudahnya perhitungan, kita gunakan saja pendekatan g = 10 m/s² . Andaikan sebuah bola dilemparkan dari puncak gedung dan diamati kecepatan dan posisinya.

Bola dilempar ke atas dengan kecepatan awal vertikal of v_yo = 20 m/s dan bergerak  juga dengan kecepatan horizontal dengan kecepatan awal horizontal of v_xo = 15 m/s.

Dalam pendekatan lain selain komponen vektor seperti di atas, kita juga dapat menggambarkan situasi ini di mana bola mempunyai kecepatan awal  v_o = 25 m/s dan membentuk sudut 53° dari horizontal. Karena sudut diukur dari horizontal, kita peroleh

v_xo = v_o cos v_yo = v_o sin

Perhatikan komponen horizontal v_x. Gerak di sini adalah gerak horizontal dengan kecepatan konstan.
Perhatikan komponen  v_y. Di sini kita melihat gerak jatuh bebas biasa dengan percepatan konstan.
Sekarang ditinjau posisi dan pergeserannya.
Perpindahan ini berasal dari komponen - x- and komponen -y persamaan,
x = x_o + v_xo t + ¹/₂ a_x t² dan
y = y_o + v_yo t + ¹/₂ a_y t²

---

Lintasan Trayektori Parabola

Gambar di samping menunjukkan model gerak parabola yang terjadi pada air mancur yang keluar dari kran air. Bentuk kurva lintasannya berbentuk Parabola.
Ketika bola dalam keadaan bergerak apakah itu karena dipukul atau dilemparkan atau disundul maka akan mengalami  gerak peluru dan mengikuti lintasan  parabola.

---

Contoh Lain

---

Contoh Lebih Lanjut  Sangat menarik untuk meninjau konsep seperti  Ketinggian Maximum  atau Jarak Maximum, disebut juga sebagai  Jangkauan Horizontal. Harap diperhatikan di sini, konsep-konsep sebaiknya janganlah dihafal begitu saja namun sebaiknya diturunkan melalui pemecahan.
Berapa jauh peluru akan bergerak?
Peluru ditembakkan dengan kecepatan awal  v_o, dengan kecepatan awal v_o dan sudut . Peluru ditembakkan dari titik asal, (x_o = 0, y_o = 0). Berapakah jauhnya peluru bergerak secara horizontal sebelum kembali ke posisi vertikalnya semula  (y = 0) kembali?
Meskipun biasanya gerak awal digambarkan dengan kecepatan awal  v_o dengan kelajuan skalar  v_o dan sudut  , terkadang lebih memudahkan untuk memecahkan persamaan dalam komponen-x- dan komponen-y kecepatan awal.
v_xo = v_o cos v_yo = v_o sin

Untuk mendapatkan Jangkau Terjauh, pertama perlu terlebih dahulu ditinjau berapa lama peluru berada di udara. Salah satu cara adalah menghitung berapa lama waktu yang diperlukan untuk mencapai puncak tertinggi. Di puncak tertinggi, komponen vertikal, komponen-y dari kecepatan bernilai nol. Selanjutnya akan diperoleh waktu yang dibutuhkan untuk  v_y menjadi nol. Selanjutnya diperlukan waktu dua kalinya untuk sampai ke tanah kembali.

Cara yang lebih langsung adalah dengan cara menghitung waktu yang dibutuhkan untuk mencapai tanah, dengan kata lain memperolah  y = 0. Gerak vertikal memenuhi rumus
y = y_o + v_yo t + ¹/₂ a_y t² di mana percepatannya adalah
a_y = - g dan
v_yo = v_o sin dan
y_o = 0 Oleh karena itu
y = 0 + (v_o sin ) t - ¹/₂ g t² Dengan men set, y = 0, dan dipecahkan untuk waktu t,
(v_o sin ) t - ¹/₂ g t² = 0 [(v_o sin ) t - ¹/₂ g t ] t = 0 Ada dua solusi,
t = 0 dan
t_tot = t = (2 v_o sin ) / g

Kedua waktu ini adalah solusi yang benar. Pertama, t = 0, mengacu ke waktu awal ketika gerak peluru mulai terlontar di  y = 0. Yang ke dua, t_tot, mengacu ke waktu ketika peluru kembali lagi ke y = 0; yang merupakan waktu yang hendak kita ketahui.

Berapa jauh  secara horizontal, peluru bergerak dalam waktu ini?
x = v_x t Range = X_max = x(t_tot) = v_xo t_tot = (v_o cos ) (2 v_o sin ) / g
X_max = 2 v_o² cos sin / g Karena persamaan mengandung suku
cos sin dan
cos = sin (90^o - ) yang berarti jangkau terjauh akan tetap sama baik untuk sudut elevasi maupun untuk sudut komplemennya (90^o -). Dengan kata lain, untuk kecepatan awal yang sama v_o, sudut elevasi  30^o dan  60^o memberikan jangkauan (titik terjauh horizontal di mana peluru menumbuk tanah) yang sama. Begitu juga untuk sudut awal  20^o dan 70^o juga memberikan jangkauan (range) yang sama.
Mengingat
2 cos sin = sin 2 Maka persamaan dapat ditulis ulang kembali sebagai
X_max = v_o² sin 2 / g Dari persamaan ini diperoleh sudut elevasi untuk jangkau paling maksimum
= 45^o karena nilai maksimum untuk sin 2 adalah 1.0 ketika  2 adalah 90^o, atau = 45^o.

---

Contoh Lain  Andaikan sebuah batu dilemparkan di dasar tebing ke puncaknya, di manakah batu tersebut akan jatuh?

Batu dilempar dengan kecepatan awal 30 m/s dengan sudut elevasi of 60^o . Sebagaimana ditunjukkan oleh gambar, batu dilempar dari dasar lembah ke udara dan mendarat di atas tebing 20 m di atas dasar lembah. Di manakah batu menumbuk tanah? Atau, seberapa jauhkah batu menempuh lintasan horizontal?

Komponen kecepatan awal:

v_xo = v_o cos v_xo = (30 m/s) (0.50)
v_xo = 15 m/s dan
v_yo = v_o sin v_yo = (30 m/s) (0.866)
v_yo = 26 m/s

Sebelum menghitung berapa jauh jarak yang ditempuh terlebih dahulu dihitung berapa lama waktu batu di udara ? Posisi-y diberikan oleh

y = y_o + v_yo t + ¹/₂ a_y t² di mana, y = 20 m.
20 m = 0 + (26 m/s) t + ¹/₂( - g ) t² 20 m = (26 m/s) t + ¹/₂( - 9.8 m/s² ) t²
20 m = (26 m/s) t - ( 4.9 m/s² ) t²
20 = 26 t - 4.9 t²
4.9 t² - 26 t + 20 = 0 Dengan memecahkan persamaan kuadrat di atas didapatkan,
t₁ = 0.9 s t₂ = 4.4 s

Secara fisis waktu  t₁ adalah waktu yang diperlukan batu melewati ketinggian tebing namun masih menanjak naik namun t₂ adalah waktu ketika batu mendarat di dataran tinggi tebing, yaitu waktu yang hendak kita cari. Jarak tempuh horizontal selama waktu ini adalah lokasi di mana batu itu jatuh dihitung mulai dari titik ia dilontarkan.

X_max = v_xo t₂ X_max = (15 m/s) (4.4 s)
X_max = 66 m